Towards Deep Learning Models Resistant to Adversarial Attacks

With adversaial attacks being considered a potentially inherent weakness in neural networks, this paper studies and optimizes the robustness of neural networks with respect to adversarial attacks. Through the authors' efforts, a reliable and "universal" solution is presented which significantly improves the resistance to a wide range of adversarial attacks.

The presenter begins with an introduction as to how adversaial attacks are conducted. Presenting a case wherein an input image is put through a CNN model to distinguish between two images: a gibbon and a panda.

By introducing noise into this model, attackers can successfully trick the model into confidently giving the wrong answer.

The presenter takes this time to show the logical flow of the presentation as it pertains to the paper.

The severity of adversarial attacks is described here. In this slide, the presenter notes that even small changes to the input image can fool state-of-the-art neural networks. He also mentions a few related works, alluding even to a few of the earlier presentations covered in this course.

On this slide, robustness is converted into an optimization problem. More specifically, this becomes a loss problem where the authors attempt to minimize risk. The new goal is to consider new adversarial inputs for training to augment the defense against future attacks.

The optimization problem becomes a saddle point problem such that it contains an inner maximization and an outer minimization problem. The problem is to find a parameter, zeta, which can yield a managed risk as well as a model which is robust against attacks.

The presenter explains the methods presented in the paper. The authors use two methods: Fast Gradient Sign Method (FGSM) and Projected Gradient Descent (PGD) to add to adversarial triaing inputs. The presenter explains how each variable is attributed to the equations. Most notable of these is epsilon which can neither be too small nor too large, otherwise it will skew the method.

At this time, the presenter makes note that the PGD method is the main contribution of the paper. He explains this alongside an explanation of an iteration of the PGD equation as it compares to the mathematics behind FGSM. He contends that PGD is more powerful because it iteratively reines the adversarial example over multiple steps. Put simply, the model improves over each iteration.

The presenter asks the class about the nature of the saddle problem: If the maximum point in the system goes down, will the other points, including the maximum, rise? Group 1 responds that they do not believe that would be the case, and the presenter agrees explainining that through PGD, a total convergence is eventually achieved.

The presenter asks a similar question relating to the optimization challenge: Will Point A go down but Point B rise? He reiterates that convergence occurs through all points in PGD.

This slide covers the challenges of the Saddle Point Problem. In outer minimization, non-convex optimizations must reduce loss. In inner maximizations, non-concave optimizations identify worst-case attacks. To mitigate these challenges, the authors proposed a tractable structure of local maxima whether the local maxima is deducible or not.

The presenter shows the two datasets used for experimentation: MNIST and CIFAR10.

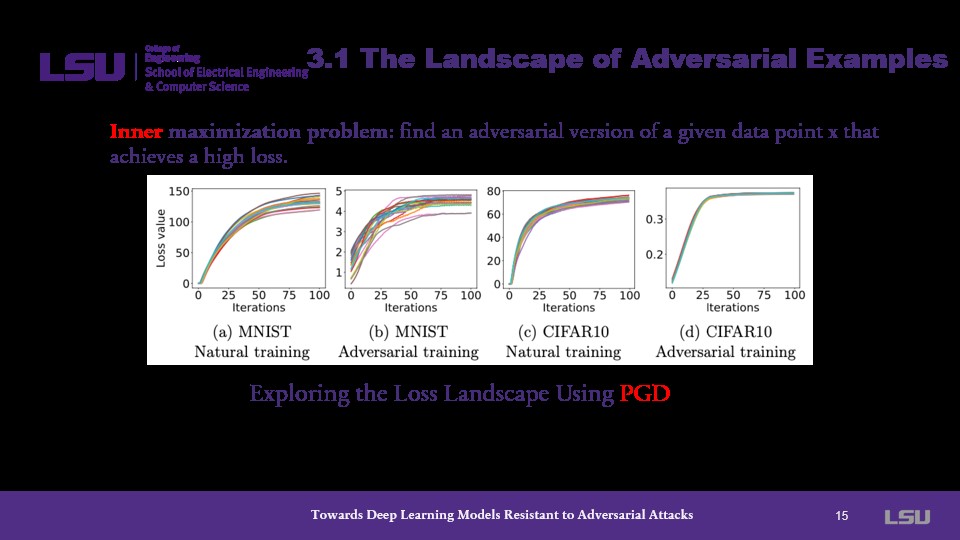
Turning to the inner maximization problem, the presenter describes a figure of the loss landscape using PGD. The figure describes experiments utilizing cross entropy loss while creating an adversarial example. In both datasets, the loss value is exponentially minimized.

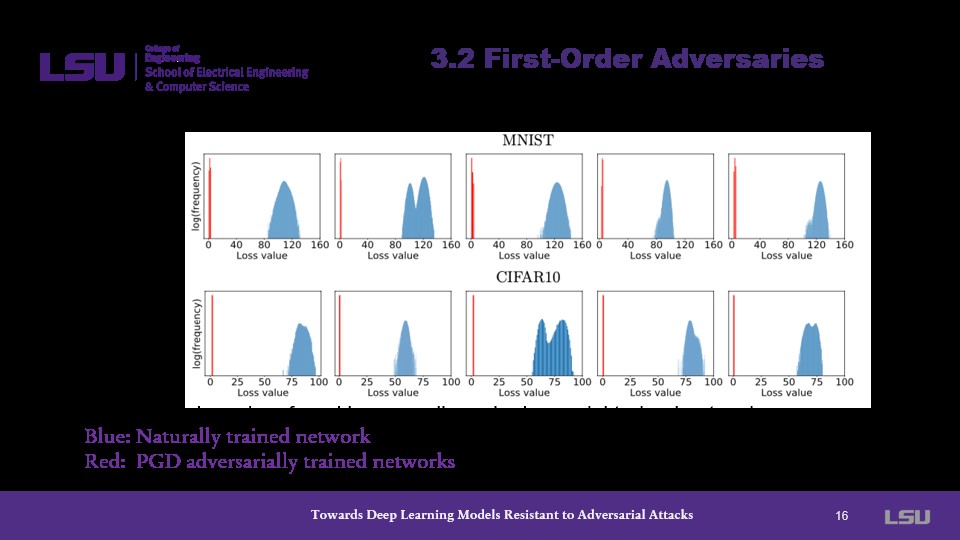
The presenter explains that "first order" refers to a catalog that adversarial attacks use in generation. Adversarial attacks rely on these first order adversaries to complete the attack. From the graph presented, the presenter shows that for both MNIST and CIFAR10, the PDG adversarially trained networks outperform the naturally trained networks.

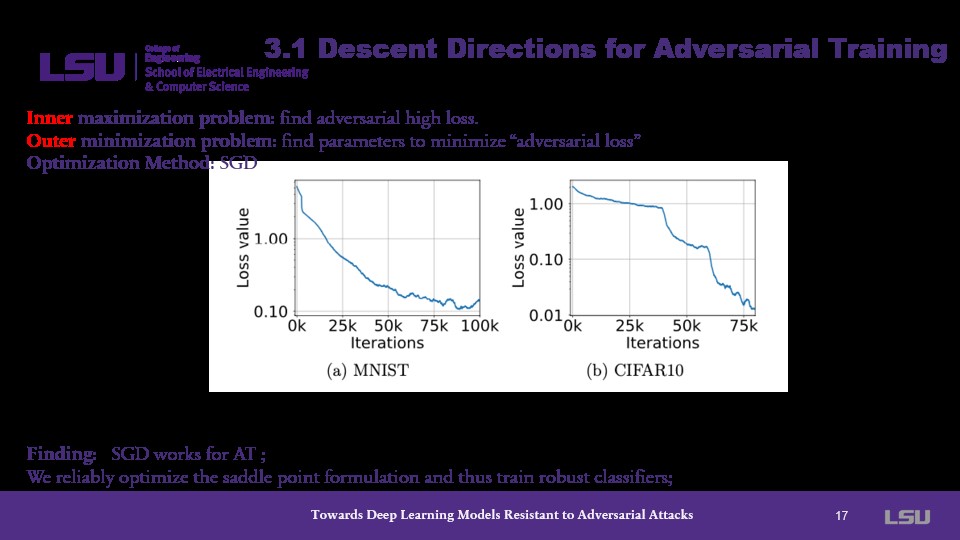
Next, attention is given to the outer minimization problem. Here, the presenter notes that Standard Gradient Descent works for adversaial training and provides a graph showing its use in minimizing "adversarial loss" through parameters. In both instances, the loss value is minimized by a factor of at least 10 across 75,000 iterations.

Classifying examples with decision boundaries is another challenge which needs adressing in this case. Separating adversaial decision boundaries becomes much more complicated as opposed to those of natural models.

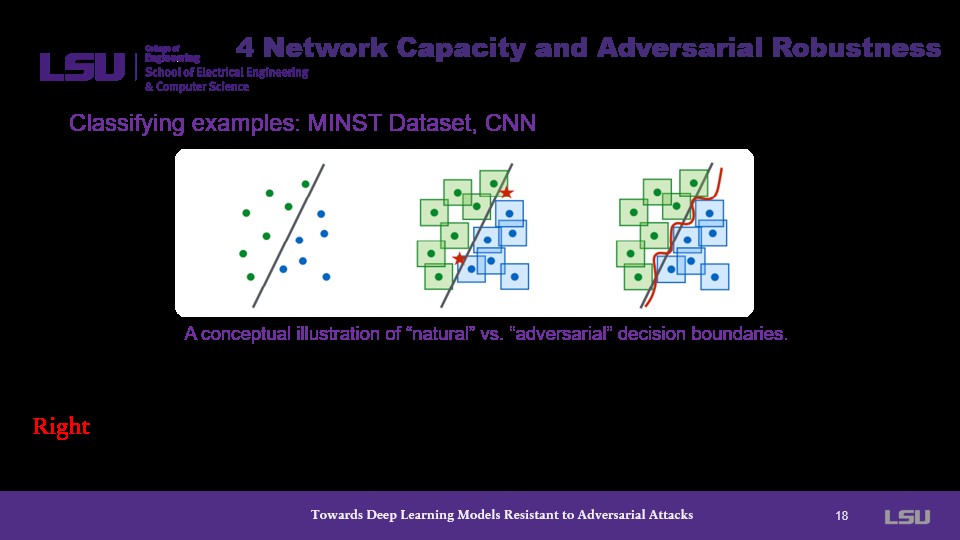
To help relieve this problem, the presenter shows that adjusting the capacity scale significantly affects the accuracy of the classifier.

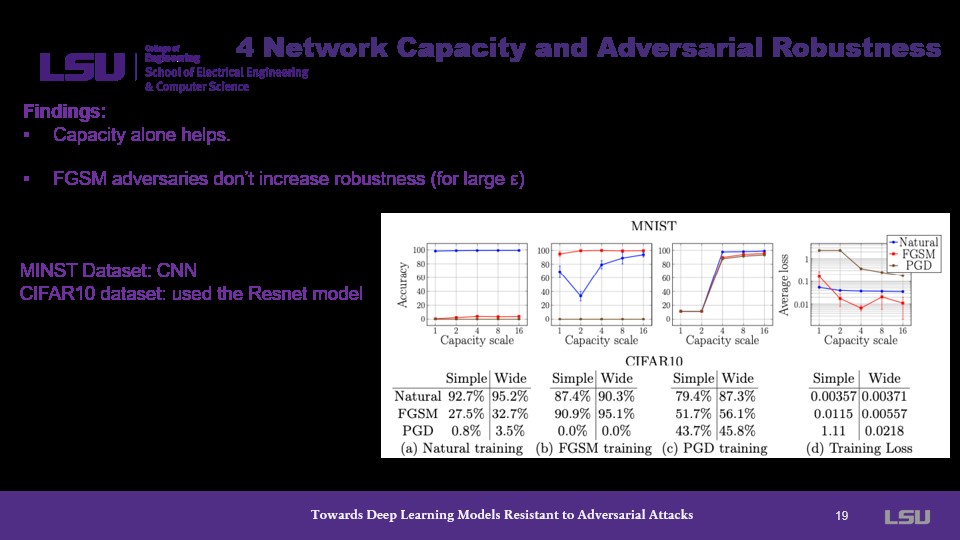
The presenter covers some tradeoffs with the capacity experiments, describing that an increased capacity decreases the value point of the saddle problem and decreases transferability of the model.

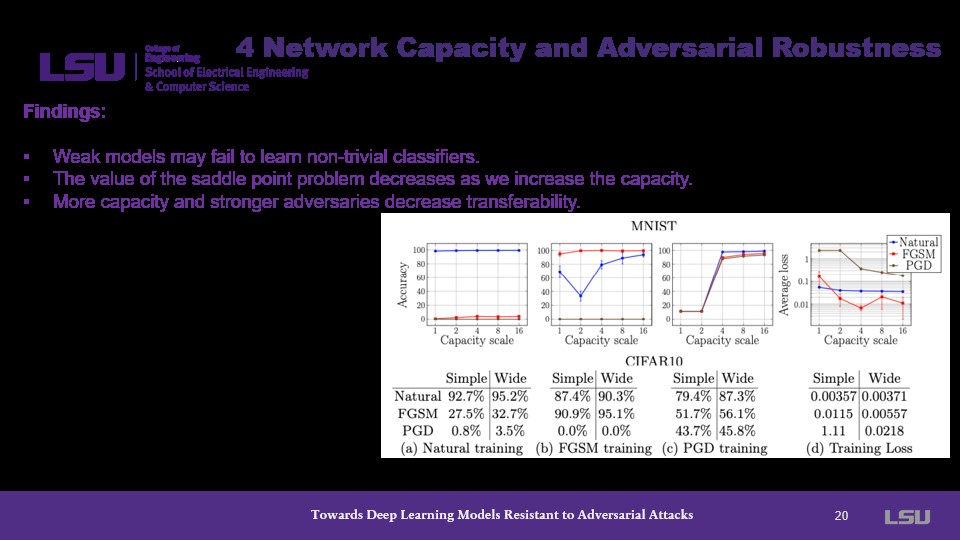
The graph presented on this slide demonstrates the effectiveness of PGD as it performs alongside several other training methods. This is done with a white-box attack which is the most efficient adversarial attack.

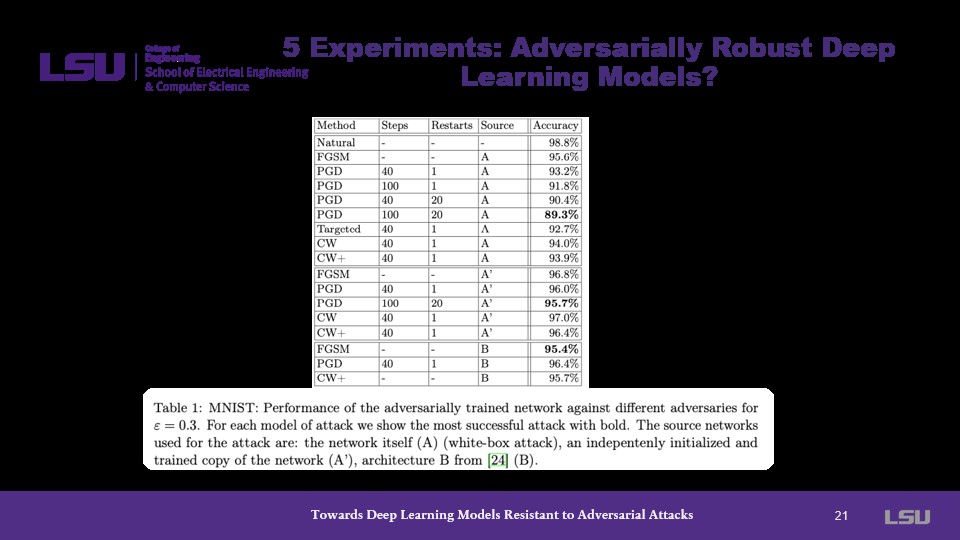
Another graph here shows similar findings to the previous slide. The presenter notes that the least amount of accuracy is desired in this instance, which PGD almost always achieves throughout experiments. This is because low accuracy in this instance means that the model is less gullible to adversarial attacks.

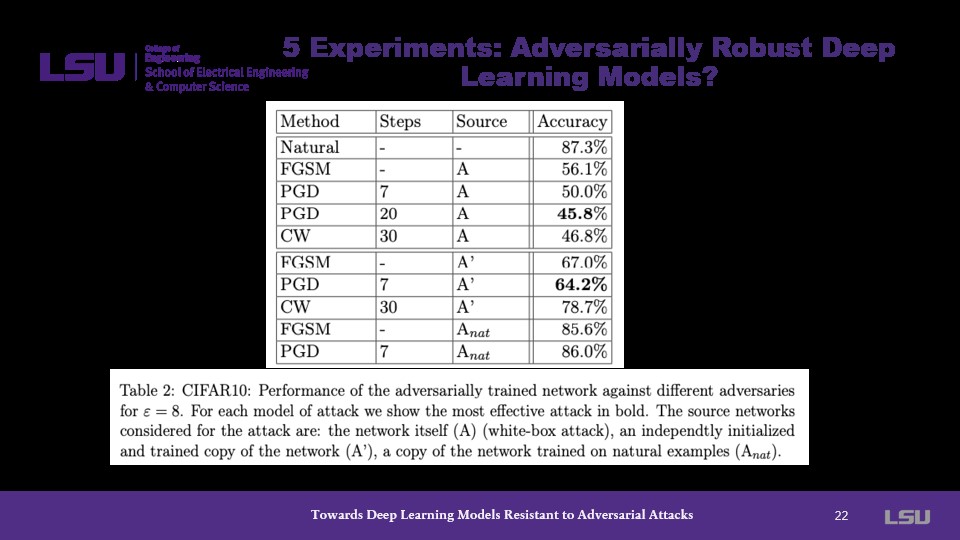
Finally, the class is shown a series of resistance charts with respect to epsilon and l2-bounded attacks. These charts show a drastic decrease in accuracy as epsilon increases. This drop is sharper in MNIST models than CIFAR10 models, but significant in both datasets.

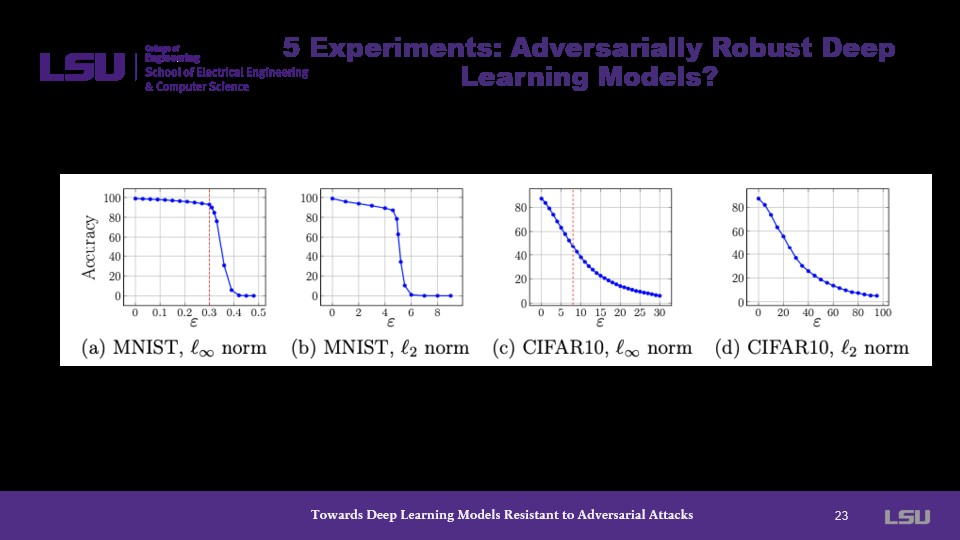
The presenter concludes the presentation by summarizing the key findings, the unexpectedly regular optimization structure, and the achievements in adversarial attack robustness.