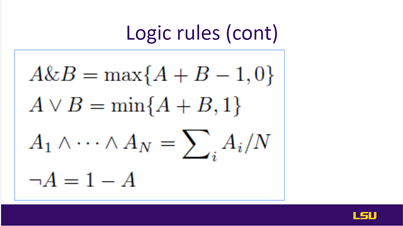Harnessing Deep Neural Networks with Logic Rules

Authors: Zhiting Hu, Xuezhe Ma, Zhengzhong Liu, Eduard Hovy, Eric P. Xing

For class: EE/CSC 7700 ML for CPS

Instructor: Dr. Xugui Zhou

Presentation by Group 9: Kendall Comeaux

Blog post by Group 5: Fozia Rajbdad

Link to Paper: https://arxiv.org/pdf/1603.06318

Research Contributions

The paper proposed a general framework for enhancing various types of neural networks (e.g., CNNs and RNNs) with declarative first-order logic rules.

Specifically, the authors developed an iterative distillation method that transfers the structured information of logic rules into the weights of neural networks.

It deployed the framework on a CNN for sentiment analysis and an RNN for named entity recognition.

This work substantially improved with a few highly intuitive rules and achieved state-of-the-art or comparable results to previous best-performing systems.

Slide 02: Presentation Outline
	The presenter introduced the presentation's layout, which included motivation, proposed methodology, possible application areas of the proposed work, results, and a discussion about the results.
Slide 03: Motivation
	The primary motivation behind the proposed work is to introduce the interpretability of deep neural networks. While deep neural networks have succeeded, there is growing concern about their black-box nature. The interpretability issue affects people's trust in deep learning systems. Secondly, deep neural networks lack the interaction of human knowledge in the model, which could be resolved to some extent by introducing human-readable logic rules in the model.
Slide 04: Introduction to Logic Rule
	The slide introduced the logic rules as a descriptive statement that describes the connection between the unknowns(variables) and constraints between them (if they exist). Moreover, it highlights that logic rules, which represent human knowledge, make constraints understandable and could work with limited label data. This offers a method of lessening reliance on deep networks based solely on data-driven approaches.

Slide 05: Objectives
	In this slide, the presenter describes the paper's primary objective: building the general framework of the DNN, which incorporates interpretability and flexibility using logic rules. This could result in reduced data labeling, improved interpretability, gaining control over the network using human-defined rules, and flexibility among various DNNs for solving different problems.
Slide 06: Framework and Method
	This slide discusses the general framework and method of the proposed work. The framework combines First-order logic rules with DNNs such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs). Iterative distillation has been used to integrate rule-based knowledge into the model weights. Secondly, in method two, networks are introduced: one teacher network that learns from the logic constraints and the other student network that imitates the prediction made by the teacher networks and progressively learns from the rule-based knowledge.
Slide 07: Knowledge Distillation
	In this slide, the presenter introduced knowledge distillation. The paper established a teacher-student model. The teacher model merges logic rules as regularization and outputs aligned with the rule constraints. Second is the student network, learned from copying teacher predictions by blending rule-based knowledge and data-driven patterns.
Slide 08: Key Components
	This slide introduces key components of the model. The first is the rule of knowledge distillation, which transfers the structured rule information to the network parameters via a teacher network constructed using the posterior regularization (PR) principle. PR, a second complement, adds logic rules as constraints during model training and ensures adherence to the desired structure. In addition, it avoids any significant increases in computational overhead. Lastly, semi-supervised learning is discussed; since the general logic rules are complementary to the specific data labels, a natural “side-product” of the integration is the support for semi-supervised learning where unlabeled data is used to absorb the logical knowledge better.
Slide 09: Framework Overview
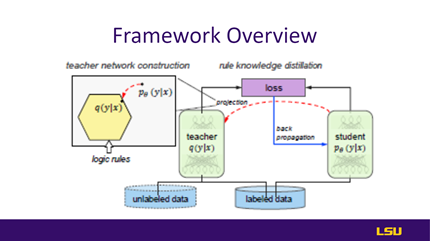
	This slide provides an overview of the framework. At each iteration, the teacher network is obtained by projecting the student network to a rule-regularized subspace (red dashed arrow), and the student network is updated to balance, emulating the teacher’s output and predicting the actual labels (black/blue solid arrows).
Slides 10 &11: Logic Rules
	This slide discusses logic rules. In the proposed work, logic rules combine traditional labeled examples with general logic rules and do not introduce extra parameters to learn. Also, rules allow truth values rather than flag values such as true or false, which helped friendly integration based on understandable values. Paper encoded the first-order logic rules using soft logic for flexible encoding and stable optimization. Specifically, soft logic allows continuous truth values from the interval [0, 1] instead of {0, 1}, and the Boolean logic operators are reformulated in slide 10.
Slides 12&13: Rule Knowledge Distillation
	In this slide, the presenter discussed the rule knowledge distillation process. The teacher network worked closely with the student network during training and guided the network toward rule-associated predictions. Whereas the student network copies the prediction made by the teacher network, it is balanced with rule-driven and labeled-data-driven learning. Secondly, the method used to create the network has been discussed. The network uses conditional probability by projecting the p(y|x) onto the rule-regulated subspace, which produces q(y|x). Furthermore, in slide 13, optimization w.r.ta to be predicted in the student network that emulates the teacher internalizing the rules has been described with the help of the equation. The new objective is then formulated as a balancing between imitating the soft predictions of q and predicting the true complex labels.
Slides 14& 18: Teacher-student Training
	This slide discusses training for the teacher-student network. In this work, teacher-student training has been done simultaneously and through an iterative learning process. In this process, teachers integrate rules into their output, while the student network aims to motivate the teacher. This enables the student network to internalize rules-based knowledge into its parameters with time through iterative guidance. Moreover, critical parameters involved in the training have been discussed in slide 18. It has been discussed that both teacher and student can be used for predictions, but the teacher network is superior to the student network. However, student networks are computationally less expensive. Similarly, pi, the imitation parameter, adjusts the focus on copying the teacher's predictions compared to learning from the labeled data. Also, it is adjusted to run time.
Slides 15 & 16: Teacher Network
	Slides 15 and 16 discuss teacher network construction. The teacher network is constructed in each iteration based on rule regularization, where predictions are projected to satisfy logic constraints. In this process, posterior regularization defines the rule-complaint prediction space. The role of the teacher network is to provide the medium for knowledge transference and teach the student rule adherence. Slide 16 demonstrates the mathematical formulation of the rules of subspace projection.
Slide 17: Distillation Algorithm
	Slide 17 summarizes the procedure of iterative distilling optimization of the proposed framework in an algorithm.
Slide 19: Semi-Supervised Learning
	This slide discusses semi-supervised learning. The proposed method can handle labeled and unlabeled data and make rules-based predictions. This method helps with limited label data to perform better, improving the generalization with reinforced logic rules.
Slides 20&21: Applications
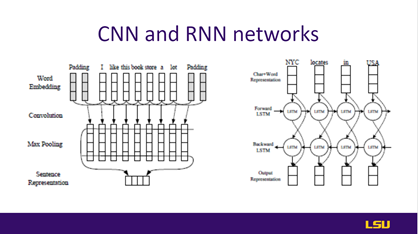
	This slide discusses potential applications where the proposed method can be helpful. These applications include semantic analysis, such as sentence-level classification with CNNs. Similarly, name entity recognition (NRE), such as sequence tagging, uses RNNs. The architecture of these networks is shown in slide 21. The CNN architecture for sentence-level sentiment analysis. The sentence representation vector is followed by a fully connected layer with softmax output activation to output sentiment predictions. Right: The architecture of the bidirectional LSTM recurrent network for NER. The CNN for extracting character representation is omitted.
Slides 22 & 23: Sentiment Analysis
	The proposed method has been used for the semantic analysis discussed in these slides. In this analysis, sentiment, both positive and negative at the sentence level, has been classified. The network design uses the convolutional layer to capture word-level sentiment features. The pooling and fully connected layers have been used to make sentence-level sentiment predictions. In slide 23, the ‘but’ rule, such as for sentences structured as A-but-B sentients, aligns with clause B, as demonstrated in the equation.
Slides 24 & 25 & 26: NER
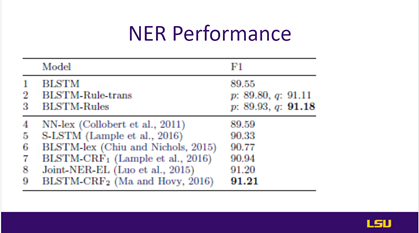
	The next application where the proposed method is used is classifying the entities in the text. The architecture consists of two networks: first, the CNN, which is used for the extraction of character and word embeddings, and pre-trained word vectors. Second is the bi-directional LSTM network, used for sequence tagging of the character and word information. Furthermore, rules used for NER are described in slide 25 and used to capture the dependencies between the outputs. Also, confidence levels are set to infinity to prevent the violations defined in the equation. In addition, rules for naming entities in lists, such as countries belonging to the same category, and similarly, rules for identifying the lists and counterparts, are also summarized with the help of the equation in slide 26.
Slide 27: Experiments
	Slide 27 discusses the experiments' details, including regularization and imitation parameters such as sentiment analysis and NER. Similarly, confidence level parameters for rules, including both soft and hard constraints, have been discussed. Lastly, Neural networks implemented using Theano trained on Tesla K40c GPU with 8-core 4.0GHz CPU and 32GB RAM have been discussed.
Slides 28-31: Results
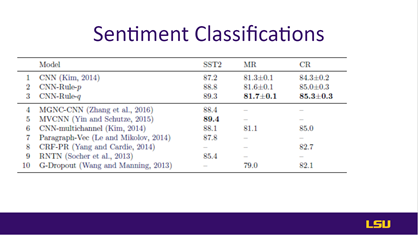
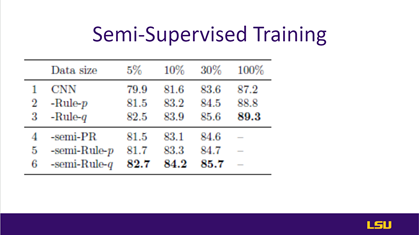
	The results of the proposed work have been discussed in slides 28-31. Sentiment classification results on slide 28 showed accuracy (%) of Sentiment Classification. Rows 2-3 are the networks enhanced by the proposed framework: CNN-Rule-p is the student network, and CNN-Rule q is the teacher network, performed better than the state-of-the-art. On slide 29, different models with their accuracy have been shown, and the proposed method achieved the highest test accuracy distilled teacher network q. on slide 30 showed accuracy (%) on SST2 with varying sizes of labeled data and semi-supervised learning. The header row is the percentage of labeled examples for training. Rows 1-3 use only supervised data. Rows 4-6 use semi-supervised learning, and the remaining training data are used as unlabeled examples. For “-semi-PR,” authors only report its projected solution, which performs better than the non-projected one. Lastly, on slide 31, the authors discussed the performance of the student and teacher models.
Slide 32: Discussion
	The presenter summarized the proposed framework, which combines deep learning and first-order logic rules, an iterative distillation procedure, and a student-teacher network.
Slide 33: Future Work
	This slide discusses potential areas for future work, such as applying the proposed network to other domains, such as computer vision and NLP. Also, rules for learning confidence levels can be obtained directly from the data, which could be a new dimension of this work's extension.
Slide 34: Teamwork
	This slide acknowledges the other team member who assisted the presenter in understanding concepts and formatting slides/discussion questions.
Slides 35 & 36: Questions and Discussions
	The last two slides showed questions and discussion from the audience about the questions and answers.

Questions:

Q1. Group 7 asked what the rule is for subspace and how it works.

Rule subspace is the projection of the teacher network on the student network.

Q2. Asked by group 7: What is the projecting weight onto the logic rule?

Projecting weights means the teacher network, i.e., the weights projected on the student constrained by a logical rule.

Q3. Asked by group 4. What is the meaning of change weights in a distillation network?

The proposed method developed an iterative distillation method that transfers the structured information of logic rules into the weights of neural networks.

Q4. Asked by Group 6: Why is a teacher network necessary?

Ans: They don’t want the student network to know the rules completely.

Discussion:

1. What do you think are the limitations of this approach in a real-world setting?

Group 1 mentioned the feasibility of using this application in the real world, especially when the rules are changed, which may not perform well.

Groups 2 and 3 have also proposed that rules included after the training models would be helpful in real-time applications.

2. Do you think this method could be used in non-text-based domains?

Group 2 proposed that gaming rules, such as chess rules, can be integrated.