A Semantic Loss Function for Deep Learning with Symbolic Knowledge

This paper discusses a method of improving the integration of symbolic logic into a neural network loss function by factoring in an additional "semantic loss function" without modifying the actual model or dataset(s) utilized. The utility of symbolic knowledge is that it improves user interpratability in the loss function without sacrificing too much accuracy, but as neural networks tend to struggle with this information being directly provided, this paper's approach helps alleviate that issue. The concept of semantic loss is described along with explanations of the experimentation on data for semi-supervised classification, as well as more complex scenarios involving reasoning.

The initial slides introduce the motivation of the cited work, notably to investigate the problem which neural networks tend to have regarding directly integrating symbolic logic into their loss functions. They generally operate on continuous values but are less suited for discrete logic-based reasoning. Some works relating to current methods of integrating symbolic logic are listed, including end-to-end learning, where the model is provided with many examples containing symbolic logic, or vector-space embedding, where symbolic logic is represented as vectors. These choices tend to address the need for differentiable models to ensure they are compatible with techniques involving gradients and/or backpropagation. However, this tends to lose the precise logical meaning of the knowledge, so the paper attempts to tackle a different approach to avoid this issue.

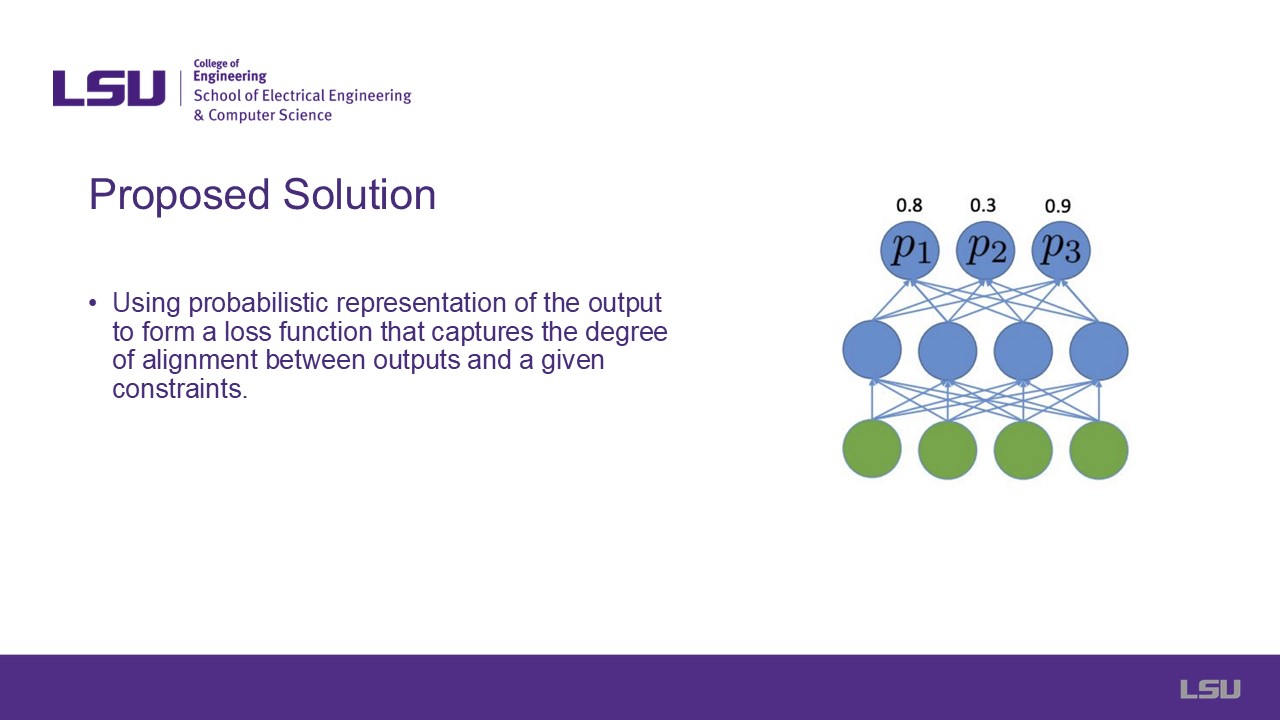
The next slide addresses the authors' proposed solution to the problem, which is to build a loss function to capture the meaning of a given constraint independent of its syntax. The method includes a probabilistic representation of the neural network outputs which can lead to any desired constraint. The idea is shown in the image to the right, where probabilities are listed in the last layer of the network.

Shown here are various symbols and lexical notations that are prevalent throughout the paper and presentation as a way to introduce the audience to some otherwise possibly unfamiliar terminology. These mostly include differences between capital and lowercase letters representing variables, and different ways to represent logical statements and operators.

After introducing terminology, the notation is then utilized to explain the paper's main contribution - the semantic loss function. The equation is shown at the bottom, along with a description above, stating that it factors in n different variables along with a vector of probabilities for each, representing each output row vector of a neural network. Each individual element in the loss function (represented using i) corresponds to a single neural network output, and this vector intends to represent how close a prediction is to having one output as true and all else as false.

Following the introduction are several properties/axioms of the semantic loss function which aim to prove the uniqueness of semantic loss. These include monotonicity, semantic equivalence, identity, satisfaction, differentiability, and ultimately uniqueness.

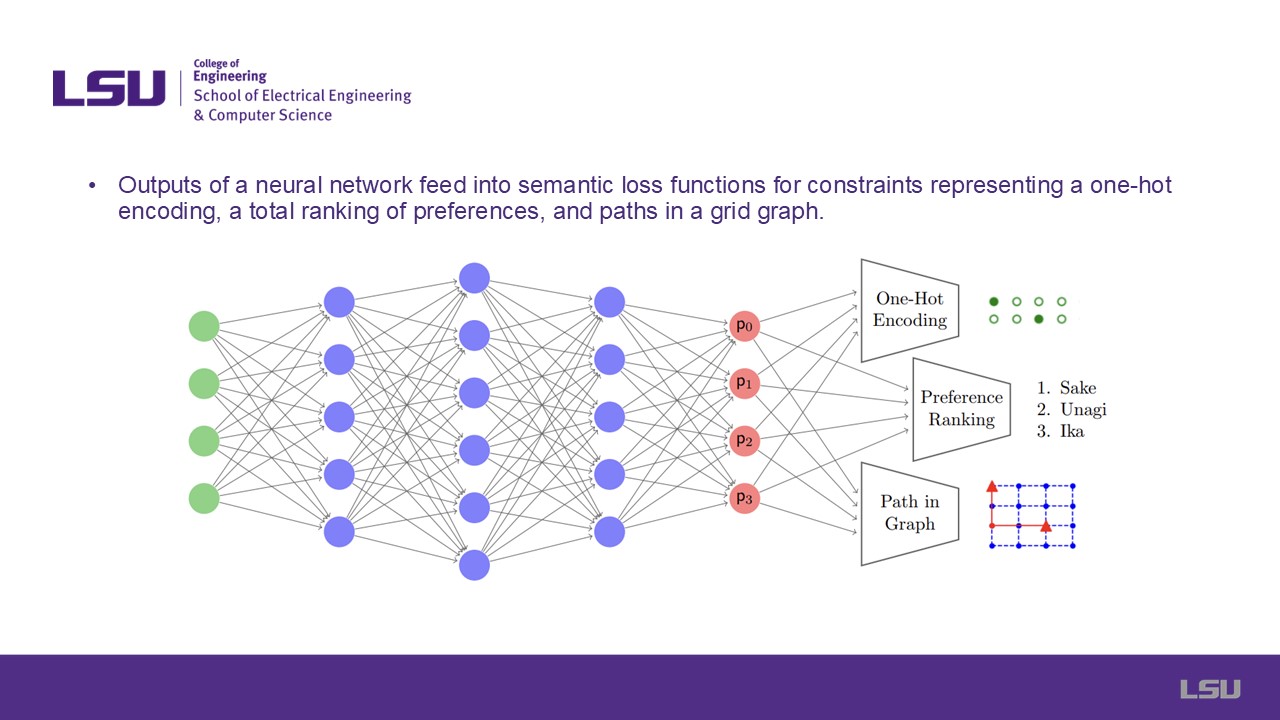
This slide shows a diagram from the paper illustrating the usage of the semantic loss functions for three different constraints appended to a neural network output layer. The probabilities can dynamically allow for the usecases of one-hot encoding, total ranking of preferences, and paths in a grid graph depending on utility and scenario need.

The presentation now begins to showcase the semantic loss function in action in various experiments, starting here with semi-supervised classification, which is claimed to be where this function is most effective. This kind of classification involves both labeled and unlabeled data, and a toy example is showcased to the right illustrating the difference between training a model with and without semantic loss integrated into its normal loss function. As shown, a more accurate decision boundary is obtained in the case using semantic loss.

This slide shares more information on how semantic loss is evaluated in semi-supervised classification against some other known methods, which is by simply adding the loss to the base models, along with the additional steps involving preprocessing, Gaussian noise, and the remaining listed steps.

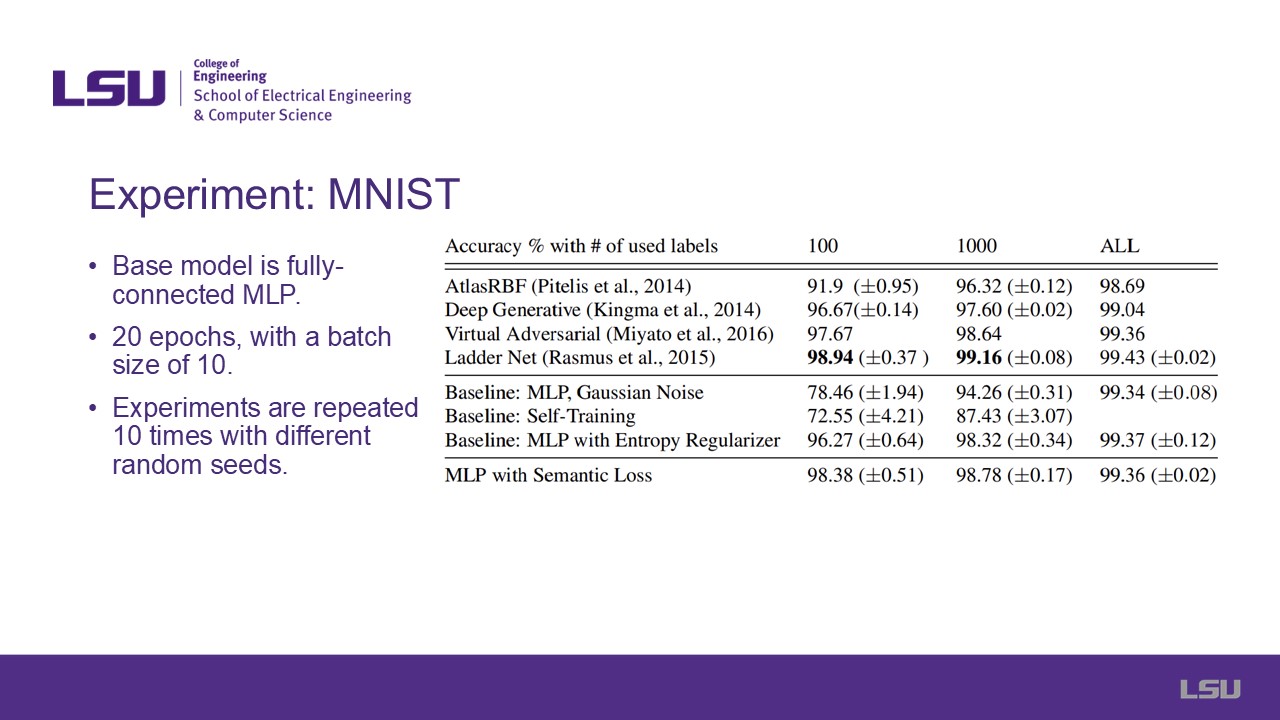
These three slides showcase three different experiments performed on well-known classification datasets including MNIST, FASHION, and CIFAR-10. Information regarding the used base models and how the experiment was performed such as number of epochs, batch size, and repetitions are included. Tables showcasing the accuracy of each selected model for each experiment is shown. For MNIST and FASHION, semantic loss is applied to a MLP, whereas a CNN is used for CIFAR-10. In general, the semantic loss model obtains the highest or nearly the highest accuracy in each experiment. However, it is important to note that maximizing accuracy is not the ultimate goal of including semantic loss, since other benefits are obtained which may sacrifice some accuracy. But since the accuracy is still almost always the highest, the results are quite positive for these specific test cases.

This slide explains how Boolean circuits can be built to represent semantic loss for more complicated constraints. A main issue with the previously discussed approach is that it only has use in semi-supervised learning and doesn't contribute much for fully supervised tasks. More complex constraints cannot be easily represented using simple boolean expressions, so these Boolean circuits can be created and then converted to arithmetic circuits to add these constraints to the loss function. This does, however, increase the time complexity to O(n^2), which is a fairly significant drawback.

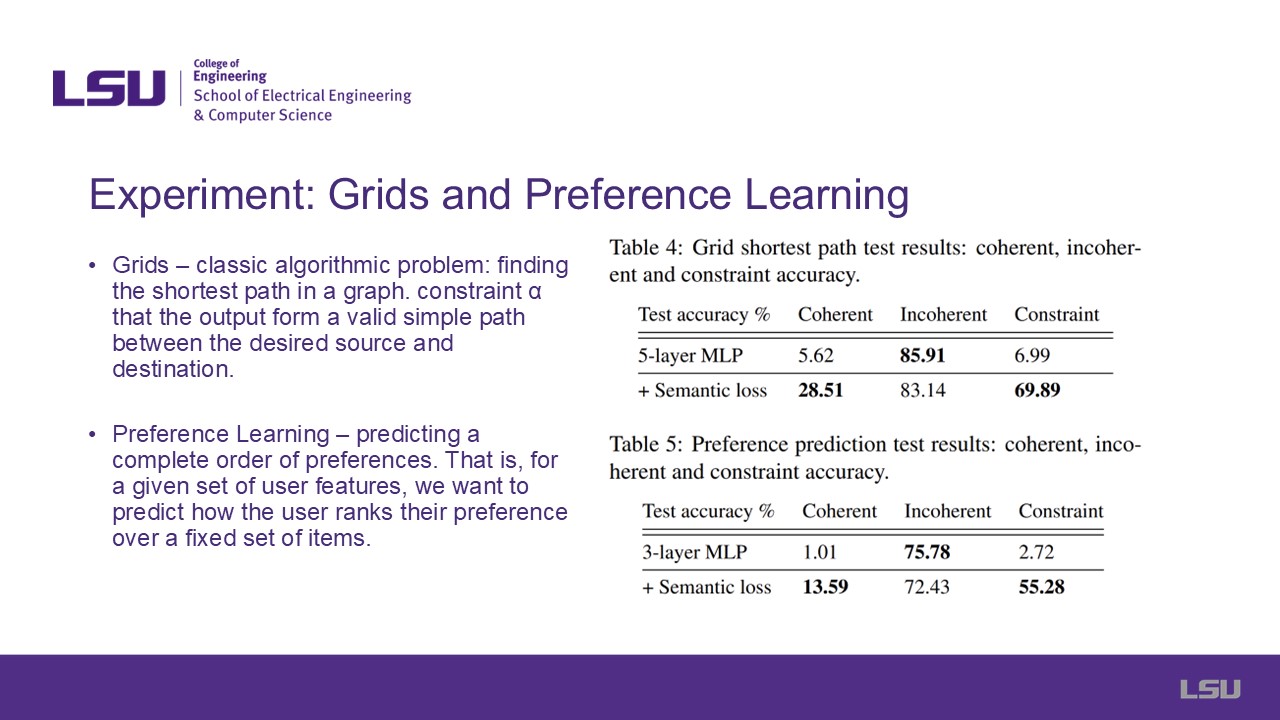
Here, two experiments are showcased involving more complex constraints, such as finding the shortest path in a grid or to predict the order of preferences on how a user would rank a list of items given a set of user features. The results are shown in the tables to the right showcasing MLPs with and without semantic loss. Coherent measures how often the model makes completely correct predictions given the set of conditions. Incoherent measures how often the model making correct predictions for each invididual part, but may not make sense when combined together. Constraint measures how often the model's predictions follow the rules/restrictions set by the problem.

This slide lists some limitations of the semantic loss concept. The first being the fact that all output domains must be fully described using Boolean logic due to the dependence on Boolean formulas and/or circuits. Secondly, the high time complexity when working with complex constraints can be computationally expensive. Lastly, the fully supervised tasks do not give much of a use to semantic loss. Ultimately, this work has not lead to much being contributed to other fields due to these limitations.

This slide acknowledges the other team members who assisted the presenter in understanding concepts and formatting slides/discussion questions.

These final slides are for questions from the audience, discussion questions for the audience, and references cited in the presentation.